“Most of the choices we make each day may feel like the products of well-considered decision making, but they’re not. They’re habits”

– Charles Duhigg, from The Power of Habit

Habits can be good or bad. Some can be helpful, while others are detrimental to our lives and profession. In this post, I question the usefulness of a geological habit universally accepted as a good thing—the geological cross-section.

Cross-sections, and their orthogonal counterpart long-sections, feature in much mining industry literature. Using a representative cross-section in a mineral resource estimation or technical report is accepted as standard industry practice. Yet the purpose of these cross-sections is never explicitly explained, even in geological mapping textbooks. Presumably, critical information about a mineral deposit is revealed to the reader by a simple glance at the geological cross-section, but is that the case?

In contrast to what we were taught at university, I suggest that geological cross-sections generally are not informative, in relation to the geometrical analysis of mineral deposits. In the mining industry, I believe that using cross-sections to interpret deposits can hinder understanding, and thus hinder exploration and resource estimation processes.
However, there is an exception—using cross-sections is generally useful in the petroleum industry (I reveal why, below). But in the minerals industry, I rarely find cross-sections geologically illuminating. In this post, I focus on their specific application to the minerals industry.

What is a geological cross-section?

Have you ever wondered why geologists in the mining industry draw cross-sections, or do you simply follow the crowd and not even question why they’re used? I suspect that this basic question doesn’t even register in many geologists’ heads; if it does, it may seem awkward or embarrassing to even raise the subject of whether cross-sections are useful.

But what exactly are we trying to achieve by drawing cross-sections? Before we can answer this question we must first define what a cross-section is. 

Cross-section – A diagram or drawing that shows features transected by a given plane; specifically a vertical section drawn at right angles to the longer axis of a geologic feature, such as the trend of an orebody, the mean direction of flow of a stream, or the axis of a fossil (Glossary of Geology, 2016). 

This definition specifically states that the cross-section must be vertical, but it also states it must be drawn at right angles to the longer axis of a geological feature. Thus, the formal definition of a cross-section is not only vertical, but is also a symmetry plane across an axial geological feature.

In my undergraduate field work, we mapped some subhorizontal folds in the field and drew a series of vertical cross-sections back at camp. Only then could we decipher the structural geometry of what we were mapping—the cross-section helped us reveal the 3D geometry of the geological features. And, as far as I could tell, that was the main benefit of drawing these vertical cross-sections.

The above definition of a cross-section works well in most undergraduate field camps where we work with simple geological structures. It also applies to most sedimentary basins where most petroleum accumulations occur, so it is sensible that the petroleum industry uses traditional cross-sections. In a foreland basin, the fold axes are horizontal, so it makes sense to draw a vertical section because that section is orthogonal to the fold thrust belt. Similar subhorizontal structural axes exist in extensional basins where strata and extensional faults intersect subhorizontally; thus the structural symmetry plane coincides with the vertical section. 

However, for most mineral deposits with more complex strain histories, the axis of a controlling structural feature is rarely horizontal. Nevertheless, mining and exploration companies produce what they refer to as ‘cross-sections’ (Figure 1); however, these rarely correspond to the definition of a cross-section (Glossary of Geology, 2016). Although the sections are vertical, rarely are they a symmetry plane of a significant linear geological feature that controls mineralisation.
 
Figure 1. South-Barnat gold deposit owned by Osisko Mining, as displayed on Corebox.net (accessed 2 May 2016). A cross-section is plotted by the Corebox.net viewer by default, which is parallel to one of the drill hole fences, but the sectional orientation can be manually moved in the viewer. The cross-section view of the deposit is shown in the lower right diagram; the position of the cross-section is shown in the upper right plan view; and in the 3D view on the left, the cross-section is shown as a shaded box.

Symmetry plane explained

Some of you may think of symmetry of structural features when I mention ‘symmetry plane’, but this isn’t what I’m referring to. Figure 2 shows a symmetric fold with orthorhombic symmetry (A) and an asymmetric fold with monoclinic symmetry (B). Both have identical fold axial orientations (red arrow), and the symmetry plane that I’m referring to is orthogonal to this axis, shown in green. This symmetry plane is also referred as the reflection plane—objects on both sides of this plane appear as a mirror image of each other.
 
Figure 2. A. symmetric fold, and B. asymmetric fold. Both have identical axial orientations (red arrow), and symmetry planes (green) regardless of their fold profile symmetry.

There’s an additional symmetry plane in the orthorhombic symmetric fold, which coincides with the axial plane. However, this plane is not orthogonal to the geological axial feature (fold axis, in this case), but instead contains the fold axis. In contrast, the monoclinic asymmetric fold has only one symmetry plane—this is the most common symmetry system we encounter in most geological situations. The best way to test if you’ve interpreted the orientation of a symmetry plane correctly is to move the plane along the interpreted axial line in a 3D viewer—objects should appear steady from one section to another. If you’re analysing grade continuity, then grade should not move around from one section to another, even if the grade terminates along the axis.

The symmetry plane of cylindrical folds is also referred to as the fold profile plane, but there’s no special geological term for the symmetry plane of other geological features, such as stock work vein systems (which can intersect along a common linear orientation).

Structural features and mineralisation patterns can be easily interpreted if the sections you’re using are parallel to the symmetry plane. If they’re not, you may not see key features in your data and therefore may not fully comprehend the mineral deposit. The amount of data is irrelevant. Even if you have a lot of data (including grade control), if you’re not using the symmetry plane to view that data, you can be lost—sometimes for many years—and end up second guessing the mineralisation controls.

Now you see it, now you don’t

To demonstrate the importance of using symmetry planes when identifying geological structure, Figure 3 shows a cross-section through a lithology model of an anonymous mineral deposit. 


General parallelism of the lithological contacts can be seen in this cross-section, but other than this, the structural patterns are not entirely obvious.

An oblique section 45° away from the vertical section in Figure 3 is shown in Figure 4. This is the symmetry section of this deposit—the structural patterns are clear, with the most obvious feature being an asymmetric intrafolial isoclinal fold at a scale similar to the mineralisation extents. 

Figure 4. Symmetry section of the deposit shown in Figure 3. The section is orthogonal to the axis of the large-scale isoclinal fold (shown in pink) seen in the centre of the image, thus orthogonal to the main structural axis of this deposit.

However, this symmetry plane is not the section the mining company geologists or academic researchers used for interpreting this deposit. Instead, geologists routinely plotted and interpreted cross-sections similar to Figure 3, and wireframed the orebody in detail in serial cross-sections. Even with dense drilling, without the symmetry plane view (Figure 4), academic researchers—as recently as 2015—concluded that this deposit was controlled by ‘secondary shear zones’, and folding or the possibility of fold-controlled mineralisation was not mentioned.

I had visited the site and folding was not thought to be an important structural control according to the majority of the site geologists, even though folds were modelled from the drill hole data during my visit (Figure 4). An experienced exploration manager with the company was nevertheless trying to convince management that folding was perhaps the major control, but without much success. Interestingly this geologist had come to this conclusion because he was studying the deposit in a 3D software package without being dependent on the cross-sectional views others were routinely using. (For those interested in reading about a non-geological and easy-to-understand example of how important symmetry sections are to interpreting 3D objects, see this post:

Carefully considered symmetry analysis is all but forgotten

Before the 1970s, the identification of symmetry styles and planes to analyse structural geometry was an important topic, as emphasised in structural textbooks and research papers (e.g. Knopf and Ingerson, 1938; Patterson and Weiss, 1961; Turner and Weiss, 1963). Older texts devoted entire chapters to the discussion of fabric and structural symmetry (Figure 5), whereas only few modern textbooks devote much space to the discussion of symmetry. An exception is a small text book by Wilson (1982) which has an excellent chapter on structural symmetry that summarises earlier pioneering works on fabric symmetry, but placing it in the context of a modern understanding of progressive strain.
 
Figure 5. The discussion of the symmetry system of folds in an early structural geology text (Knopf and Ingerson, 1938, p. 57).

Bruno Sander proposed that the fabric symmetry of deformed rocks reflects the kinematic history of deformation (Sander, 1930); therefore, identifying and documenting fabric symmetry was a critical first step in analysing deformed rocks (Figure 6A).

Figure 6. The documentation of symmetry of deformed rock masses has decreased significantly since the 1970s. A) Symmetry analysis was considered crucial to establishing kinematics before the 1970s. B) Since the 1970s, there has been a significant increase in interpreting kinematics without clearly establishing 3D symmetry from geological data.

The discussion and emphasis on the symmetry of geological structures had been slowly declining before I started my geological education in 1981 (Figure 6B).  Since joining the mining industry in 1999, I haven’t met a single geologist who has even mentioned this subject in the context of the analysis of mineral deposits. This is despite the mining industry analysing 3D drill hole data more than ever before. In today’s data-rich environment we depend on computerised data-mining and artificial intelligence methods to extract the patterns we need for mining and exploration. But we’ve forgotten the very effective techniques of identifying symmetry patterns that exist in deformed rocks that control mineralisation. Symmetry analysis—an essential skill considered a prerequisite of kinematic analysis, and developed nearly 90 years ago—is no longer part of the lexicon of modern geologists.

As pointed out by Ramsay (1967) and Siddans (1972), the inference of kinematics from the observation of structural symmetry is not as straight forward as what Sander had envisaged.

We’re almost two generations removed from when symmetry analysis was considered an important methodology, and now the general mining community is ignorant of this cornerstone subject of modern structural analysis.  However, the emphasis of this post is the fact that the mining industry as a whole routinely ignores symmetry of mineral deposits even though this can be readily documented.

This is despite the fact that most mineralised trends mimic the underlying structural symmetry of host rocks.

We’re almost two generations removed from when symmetry analysis was considered an important methodology, and now the general mining community is ignorant of this cornerstone subject of modern structural analysis.

Despite this, structural geologists do intuitively use symmetry patterns to guide their kinematic interpretation of micro- and mesoscopic structural features. However, their application of the symmetry principle stops short of analysing mineralisation at the scale of the entire deposit. They rarely look at mineralisation patterns to inform them of structural symmetry, but instead scale up outcrop and core structural observations to the scale of the deposit. Such habitual scale-invariant structural analysis is performed routinely even though high-resolution data such as grade control are available at most mines to cross-check their interpretations. Grade control is a valuable dataset that can inform us of the symmetry of mineral deposits, but because grade control data are not considered by structural geologists to be ‘structural data’, these data are largely unexamined by these geologists. It is not uncommon for the symmetry of mineral deposits, and therefore the controls of mineralisation, to go unnoticed for many years.

And that is the crux of the problem with traditional cross-sections—the geological patterns that need to be conveyed cannot be understood if the cross-section is not a symmetry plane of the 3D mineralisation pattern.

After examining and modelling many hundreds of mineral deposits, I’ve concluded that the example illustrated in Figure 3 is not an isolated incident; instead, situations like this are very common, if not the norm.

If you doubt my conclusion, think of a deposit you worked on recently. Determine the axis of the deposit and specify what structural controls are responsible for the mineralisation that resulted in this symmetry pattern. Every deposit exhibits a symmetry pattern, and the symmetry pattern is a clue to the structural control of the deposit (see Figure 7). However, it is highly likely that you can’t describe the symmetry of the deposit because you’ve simply not thought about it. Without knowing the symmetry, you won’t know what controlled the mineralisation. That lack of knowledge will then affect your exploration and resource evaluation processes.

Figure 7: A selection of fabric symmetries of geological structures (Cowan, 2014): a) bedding fabric representing axial symmetry, but linear axis is absent; b) pure linear fabric with axial symmetry; c) sheath fold with extreme stretch representing orthorhombic symmetry; d) conjugate fault system with orthorhombic symmetry; e) upright fold with orthorhombic symmetry; f) faulted bedded fabric with monoclinic symmetry; g) C-S fabric with monoclinic symmetry; h) overturned folding with monoclinic symmetry; i) multi-phase folding with triclinic symmetry. All examples except (a) and (i) display a first-order linear fabric (of either elongation or intersection lineation) that is orthogonal to the symmetry plane. In (a) linear fabric is absent, and in triclinic fabric (i) there may be local linear axes as indicated by the arrows.

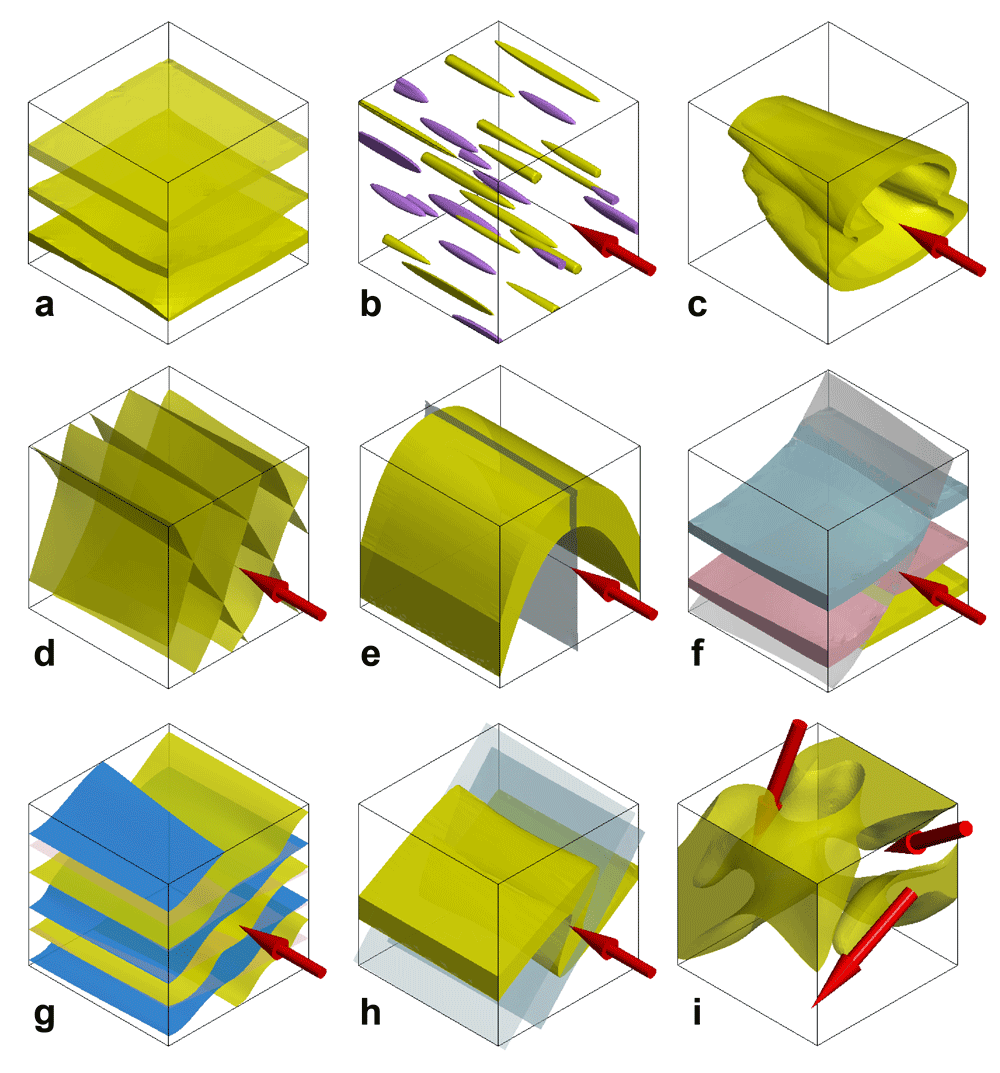
Cross-sections and symmetry planes are not generally parallel to each other

Figures 8 to 12 illustrate typical examples of mineral deposits with their default cross-section orientations (purple) (i.e. parallel to drill hole fence) and the symmetry plane (green). 

Figure 8.

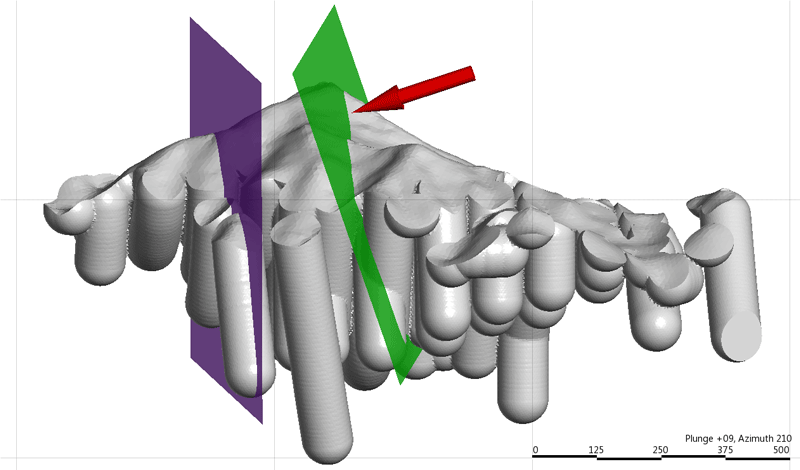
Figure 9.

Figure 10.

Figure 11.

 

Figure 12.

The linear structural axis, coincident with the long axis of mineralisation, is parallel to the red arrow. The deposit shown in Figure 8 only has a 10° obliquity between the cross-section plane and the symmetry plane, so cross-sections may be used to interpret this deposit. Other than this deposit, none of the others (Figures 9 to 12) are suitable for geological interpretation using traditional cross-sections parallel to the drill hole fences. This non-parallelism between cross-sectional planes and the symmetry section is typical of most mineral deposits.

Conclusion

I’ve found that not using or relying on cross-sections speeds up geological interpretation processes and significantly increases geological modelling accuracy, as well as improving geological understanding of deposits. In 2001 I realised that vertical cross-sections are just a habit, so I stopped using them, at least for the analysis of mineral deposits. I’ve interpreted and built implicit geological models of more than 600 mineral deposits since 2001; conversely, the number of models I’ve generated using cross-sections are relatively few because the cross-sectional plane is not generally parallel to the deposit symmetry plane. 

In my recent post on Taking Advantage of Geological Bias, I explained that consciously considering the opposite of what most geologists do may lead you to a surprising discovery and sometimes a much better analytical methodology.  Ignoring cross-sectional views is one such example that has worked for me.

---

Jun Cowan, PhD, is a director and principal structural geologist of consulting firm Orefind, and the conceptual founder of Leapfrog geological modelling software. He holds an Adjunct Senior Research Fellow position at the School of Geosciences, Monash University.

Based in Fremantle, Western Australia, Orefind is a geological consulting company founded by structural geologists Brett Davis and Jun Cowan.

This post is reproduced as a LinkedIn post. Constructive feedback are always appreciated on LinkedIn.

References

Cowan E J, 2014. ‘X-ray Plunge Projection’— Understanding Structural Geology from Grade Data. AusIMM Monograph 30: Mineral Resource and Ore Reserve Estimation — The AusIMM Guide to Good Practice, second edition, 207–220.

Glossary of Geology, 2016. American Geosciences Institute. Fifth Edition.

Knopf E B, and Ingerson E, 1938. Structural Petrology. Geological Society of America Memoir, 6. 270p. (Geological Society of America, Washington).

Patterson, M S and Weiss L E, 1961. Symmetry concepts in the structural analysis of deformed rocks. Geological Society of America Bulletin, 72: 841–882.

Ramsay, J G, 1967. Folding and Fracturing of Rocks. 568pp. (The Blackburn Press: Caldwell).

Sander, B, 1930. Gefügekunde der Gesteine. 352p (Springer: Vienna).

Siddans, A W B, 1972. Slaty Cleavage – A Review of Research Since 1815. Earth-Science Reviews, 8, 205-232.

Turner, F J and Weiss, L E, 1963. Structural Analysis of Metamorphic Tectonites. 545p. (McGraw-Hill: New York).

Wilson, G., 1982, Introduction to Small-Scale Geological Structures. 128p (George Allen & Unwin: London).